Feature Interaction Importance provides full transparency into interactions between all model's features, combined with the ability to sort, filter and rank these bi-variate interactions. The interactions are ranked by Importance Measure to zero in on the most important bi-variate interaction.
Generating data: If this is the first time the interaction importance data is being requested, the data need to be generated first by clicking the "Generate Interaction Data" button. The below prompt will come up:
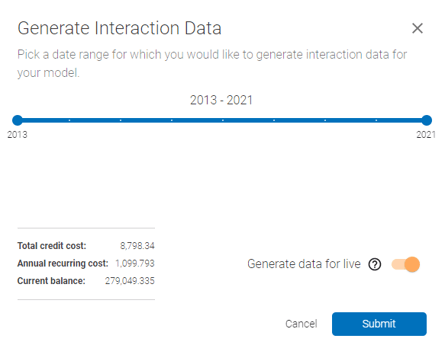In the above prompt, select the date range and enable/disable generation for live portion of the model - this will generate the data automatically for live model every time the model is re-trained, at the frequency that is pre-defined at setup.
Interpretation:
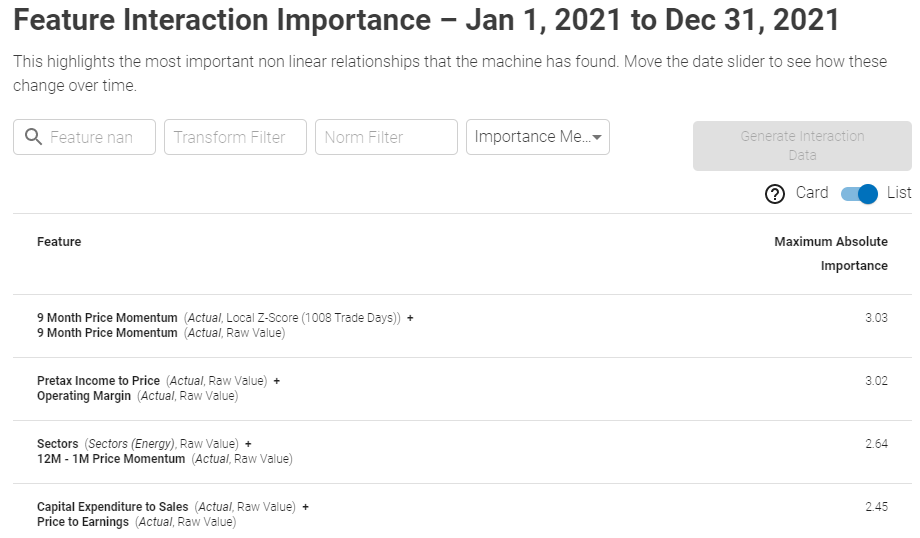
The screen can be presented in both a list and card view, ranked by the importance measures as shown below:
List View:
Showcases bi-variate feature interactions, ranked by Importance
Card View:
Showcases bi-variate feature interactions in an intuitive card view. Y axis represents the Buy/Sell signal strengths, first feature is plotted on X axis and dot color gradient from blue (low) to orange (high) represents the value of the second feature.
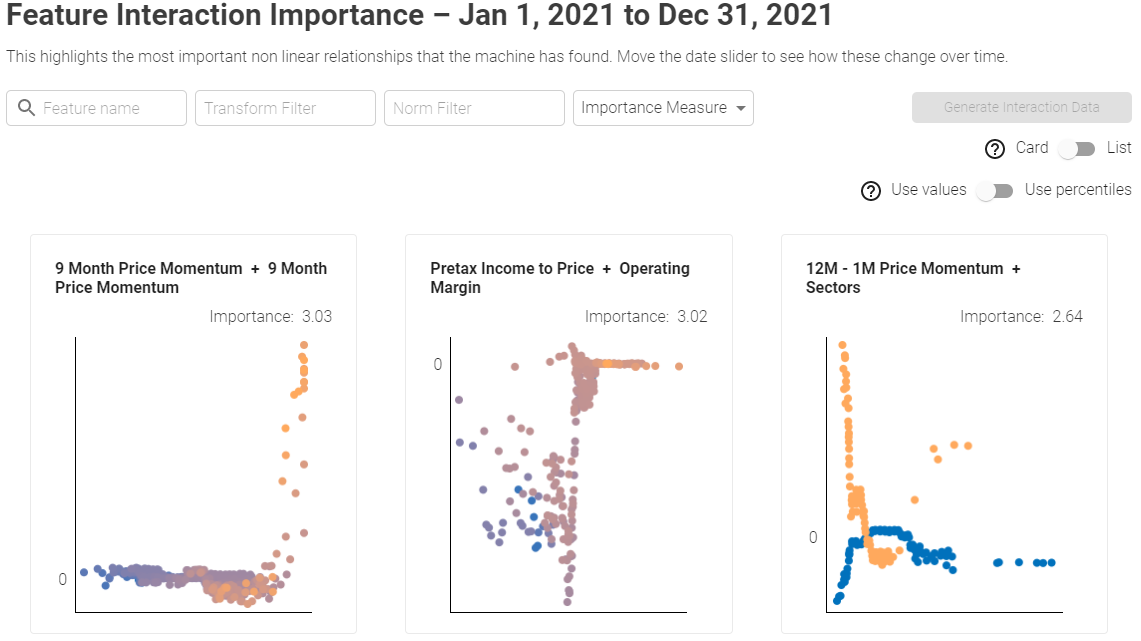
The search bar at the top that can be used to narrow down the features to only the ones of interest. User can also filter by Transformation and Normalization. For example you can filter only Absolute values (Transformation) and Local Z-scores (Normalization).
Lastly, the Importance Measure could be either the Maximum Absolute value or the Mean Absolute value, such as:
Interpreting two-factor interactions: clicking on each individual row or card will bring up a pop-out with detailed bi-variate chart.
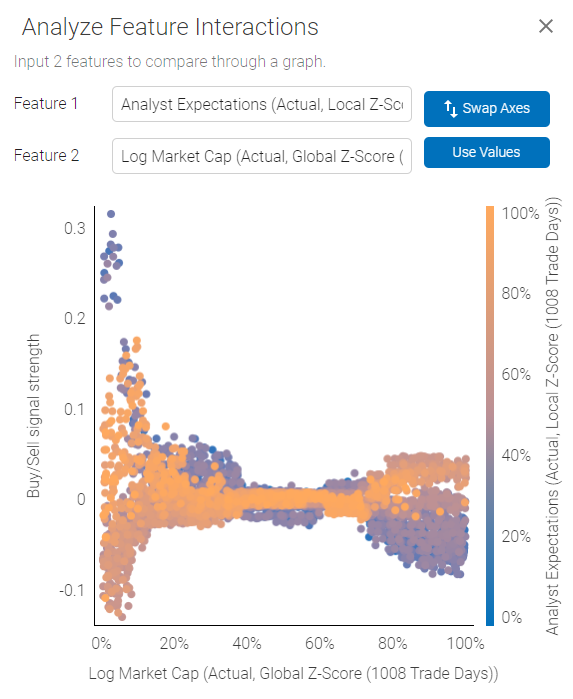The plot demonstrates how the two selected features interact in relation to Buy/Sell signal strength.
Using the plot above as an example - we are looking at an interaction between Analyst Expectations and Log Market Cap. Analyst Expectations are represented by the color scale on the right, Log Market Cap is plotted on the X axis and Buy/Sell signal on the Y axis.
The plot shows us that Analyst Expectations are somewhat weakly correlated with a Buy/Sell signal for high Market Cap companies, and there is less scatter, outcome are more uniform for high Market Cap stocks. However, high Analyst Expectations for smaller companies could actually be a Sell signal, while low expectations for small companies could generate a strong Buy.
Note:
1) Axes can be swapped to get different perspective on the interactions.
2) Axes can be plotted based on Value or Percentiles, which normalizes factor values for potentially cleaner representation.
3) For binary variables (True / False) such as Sectors - value of 1 (bright orange) will represent True and 0 will be false.