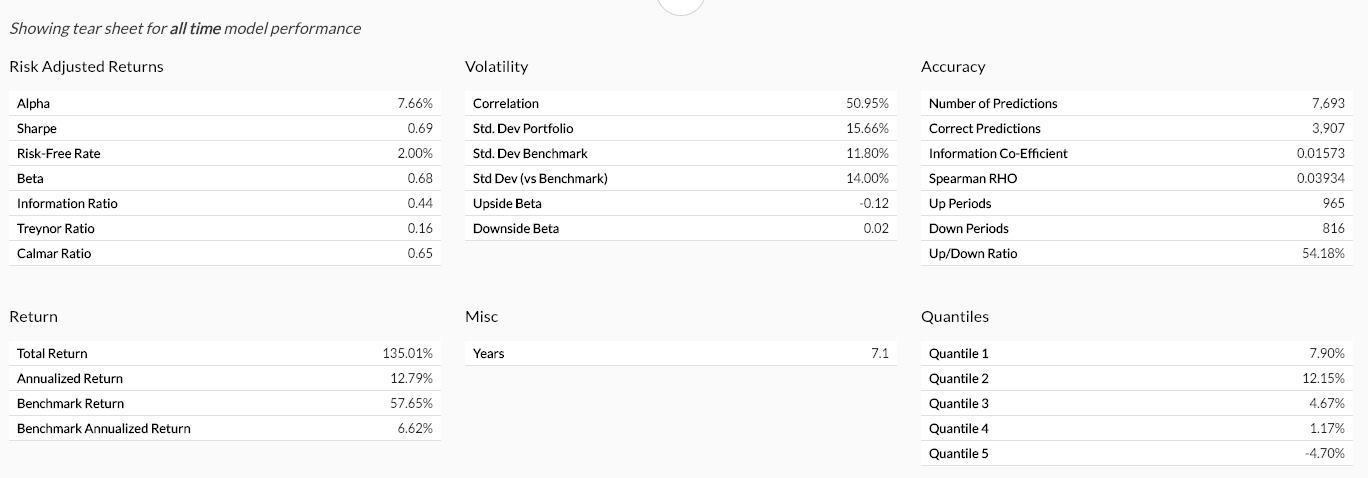
样表包含模型在所选图形范围内的关键绩效指标。
“准确率 (Accuracy)”和“分位数 (Quantiles)”指标是基于原始模型的股票排名输出,不会因为投资组合设置的改变而改变。为提高准确率,需要创建并训练新模型。
“收益率 (Returns)”和“波动率 (Volatility)”指标是基于投资组合的整体表现,会随着投资组合设置的修改而改变。(请参阅关于投资组合设置的更多信息)
风险调整后收益率细分
|
|
说明 |
|
年化阿尔法(Annualized Alpha) |
阿尔法 = 年化收益率 - 无风险利率 -(贝塔 * (基准年化收益率 - 无风险利率))。
阿尔法是一项投资的主动收益率的衡量指标,即该投资与合适的市场指数相比的表现。阿尔法为 1%,意味着该投资在选定的一段时间内的投资收益率比同期的市场好 1%;阿尔法为负数,意味着该投资的表现低于市场。 |
|
夏普比率 (Sharpe) |
夏普比率 =(年化收益率 - 无风险利率/投资 组合的标准差
夏普比率衡量的是一项投资(如证券或投资组合)与无风险资产相比,在调整其风险后的表现。 |
|
无风险利率 (Risk-free Rate) |
无风险利率 = 0.5
无风险利率是指在一段固定时间内有计划付款的假设投资的收益率,并假设该投资满足所有付款义务。 |
|
贝塔 (Beta) |
贝塔 = 相关系数 *(投资组合的标准差/基准的标准差)
贝塔是因受一般市场波动而非特殊因素影响而产生的风险的衡量指标。 |
|
信息比率(Information Ratio) |
信息比率 =(年化收益率 - 基准年化收益率)/((投资组合收益率- 基准收益率)的标准差)
信息比率衡量和比较一项投资(如证券或投资组合)与基准指数相比的主动收益率相对于主动收益率的波动率(也称为主动风险或基准跟踪风险)的比率。它代表了投资者每增加一个单位的风险所获得的额外收益。 |
|
特雷诺比率(Treynor Ratio) |
特雷诺比率 =(年化收益率 - 无风险利率)/贝塔
特雷诺比率是每单位承担的市场风险所获得的收益率超过没有可分散风险的投资(如国库券或完全分散的投资组合)可能获得的收益率的衡量指标。 |
|
卡尔玛比率(Calmar Ratio) |
卡尔玛比率 =(年化收益率/最大回撤的绝对值)
卡尔玛比率是基金平均复合年收益率与最大回撤的函数。卡尔玛比率越高,在给定的时间范围(通常设定为 36 个月)内,其风险调整后的表现越好。 |
收益率细分
|
|
说明 |
|
总收益率 (Total Return) |
总收益率 =(投资组合在结束日期的价值 - 投资组合在开始日期的价值)/投资组合在开始日期的价值
投资组合的总收益率不仅要考虑投资组合的资本增值,还要考虑投资组合的收入。收入一般包括利息、股息和证券借贷费用。 |
|
年化收益率(Annualized Return) |
年化收益率 =(1 + 总收益率)^(1/年数)- 1
年化收益率是指以年为单位计算的总收益率,以便比较可能跨越不同时期的收益率。 |
|
平均实际股息率(Avg. Actual Dividend Yield) |
平均 实际股息率 = 投资组合实际观察到的股息率
股息率是指每股的股息除以每股的价格。对于实际股息率,我们是跟踪实际收到的股息,所以第 1 天的股息率是 0,到第 1 年年底就会上升到实际股息率。 |
|
平均隐含股息率(Avg. Implied Dividend Yield) |
平均 隐含股息率 = 基于投资组合中所有股票历史加权股息率的隐含股息率
平均隐含股息率是指通过计算投资组合中所有股票的历史加权股息率可能达到的股息率。 |
|
基准收益率(Benchmark Return) |
基准收益率 =(结束日期的基准价格 - 开始日期的基准价格)/开始日期的基准价格
基准收益率是指基准的总收益率。它不仅考虑到投资组合的资本增值,还考虑到投资组合的收入。收入一般包括利息、股息和证券借贷费用。 |
|
基准年化收益率(Benchmark Annualized Return) |
基准年化收益率 =(1 + 基准收益率)^(1/年数)- 1
基准年化收益率是指以年为单位的基准收益率。 |
|
平均基准股息率(Avg. Benchmark Dividend Yield) |
基准股息率 = 基准的 平均实际股息率
基准股息率是基准的平均实际股息率。对于实际股息率,我们是跟踪实际收到的股息,所以第 1 天的股息率是 0,到第 1 年年底就会上升到实际股息率。 |
波动率细分
|
|
说明 |
|
相关系数(Correlation) |
相关系数 = 按天计算的期间收益率与按天计算的基准收益率的相关系数
相关系数衡量两个或两个以上的金融变量随时间变化的关系。例如,股票和固息债券的价格经常朝相反的方向变动:当投资者卖出股票时,他们经常用收益购买债券,反之亦然。在这种情况下,股票和债券价格是负相关的。 |
|
投资组合标准差(Std. Dev Portfolio) |
投资 组合标准差 = 按天计算的期间收益率的标准差 * SQRT (252)
投资组合的标准差是衡量投资组合收益率相对于其均值的分散性的统计量,其计算方法是方差的平方根。它是通过确定每个数据点之间相对于均值的差异来计算方差的平方根。如果数据点离均值越远,数据集内的偏差就越大;因此,数据越分散,标准差就越大。 |
|
基准标准差 (Std. Dev Benchmark) |
投资 标准差 = 按天计算的基准收益率的标准差 * SQRT (252)
基准的标准差是衡量基准相对于其均值的分散性的统计量,其计算方法是方差的平方根。它是通过确定每个数据点之间相对于均值的差异来计算方差的平方根。如果数据点离均值越远,数据集内的偏差就越大;因此,数据越分散,标准差就越大。 |
|
标准差(相对于基准)(Std. Dev (vs Benchmark)) |
投资 差(相对于基准) = 投资 组合收益率的标准差 - 基准收益率
相对于基准的标准差,又称为跟踪误差,是投资组合中因投资组合经理作出的主动管理决策而产生的风险的衡量指标;它表明投资组合跟随其基准指数的密切程度。 |
|
上行贝塔 (Upside Beta) |
上行贝塔 = 只计算上涨日的贝塔
上行贝塔是传统贝塔的要素,投资者通常不会将其与风险的真正含义联系起来。它是指某一资产与基准相比趋向于变动的缩放金额,仅在基准收益率为正的日期计算。 |
|
下行贝塔(Downside Beta) |
下行贝塔 = 只计算下跌日的贝塔
下行贝塔是贝塔的要素,投资者将其与风险(即不确定的潜在损失)联系起来。它是指某一资产与基准相比趋向于变动的缩放金额,仅在基准收益率为负的日期计算。 |
杂项 细分
|
|
说明 |
|
总周转率 (Total Turnover) |
总周转率是指周转金额相对于投资组合的股本的比率,以买入为衡量指标。如果您有 100 美元的股本,买入 100 美元的证券,卖出 100 美元的证券,则您的周转率为 100%。 |
|
年周转率 (Annual Turnover) |
年周转率是指总周转率除以模型的活跃年数。 |
|
年数 (Years) |
年数 = 以天为单位计算的(模型的结束日期 - 模型的开始日期)/365
简单来说,年数就是投资组合跨越的年数。 |
准确率细分
|
|
说明 |
|
预测次数 (Number of Predictions) |
预测次数 = 总交易次数
简单来说,预测次数就是一段时间内机器推荐的交易次数。 |
|
正确预测次数(Correct Predictions) |
正确预测次数 = 有正收益的交易次数
正确预测次数是收益高于基准的推荐交易次数。 |
|
信息系数(Information Co-Efficient) |
信息系数 = 2 *(正确预测次数/预测次数)- 1
信息系数是预测值优劣的衡量指标。在金融领域,信息系数用作衡量金融分析师预测能力的绩效指标。信息系数类似于相关系数,可以看作两个随机变量(例如预测的股票收益率和实际收益率)之间线性关系的衡量指标。信息系数的范围为 0 至1,0 表示预测值与实际值之间没有线性关系(预测能力差),1 表示有完美的线性关系(预测能力好)。 |
|
斯皮尔曼等级相关系数 (Spearman RHO) |
斯皮尔曼等级相关系数 = ML 等级顺序的相关系数
预测次数与股票收益率等级顺序之间的斯皮尔曼等级相关系数,以查尔斯·斯皮尔曼 (Charles Spearman) 的名字命名,是等级相关性(两个变量的等级之间的统计依赖关系)的非参数衡量指标。它评估使用单调函数描述两个变量之间关系的程度。 |
|
上涨期 (Up Periods) |
上涨期 = 收益率为正的天数
简单来说,上涨期就是统计期内收益率为正的天数。 |
|
下跌期 (Down Periods) |
下跌期 = 收益率为负的天数 简单来说,下跌期就是统计期内收益率为负的天数。 |
|
涨跌比率 (Up/Down Ratio) |
涨跌比率 = 上涨期/(上涨期 + 下跌期)涨跌比率描述的是收益率为正的天数占总交易天数的百分比。 |
收益率分位数细分
|
|
说明 |
|
收益率分位数(标题)(Return Quantiles (Title)) |
收益率分位数是此模型内排名最高和最低的股票。对于同一模型内的新投资组合,这些不会改变。分位数 1 的股票排名 5 星,分位数 2 的股票排名 4 星,以此类推。
“几何平均收益率 (Geometric Mean Return)”主要用于复利投资,用于计算多期复利投资的每期平均收益率。我们对每个分位数进行计算。 |
|
分位数 1 (Quantile 1) |
排名 5 星的股票。这部分股票是我们的机器学习认为表现最好的股票。
分位数 1 =(第一个分位数的几何日收益率)^ (252/1) - 1 |
|
分位数 2 (Quantile 2) |
排名 4 星的股票。这部分股票是我们的机器学习认为表现比平均水平好的股票。
分位数 2 =(第二个分位数的几何日收益率)^ (252/1) - 1 |
|
分位数 3 (Quantile 3) |
排名 3 星的股票。这部分股票是我们的机器学习认为表现一般的股票。
分位数 3 =(第三个分位数的几何日收益率)^ (252/1) - 1 |
|
分位数 4 (Quantile 4) |
排名 2 星的股票。这部分股票是我们的机器学习认为表现低于平均水平的股票。
分位数 4 =(第四个分位数的几何日收益率)^ (252/1) - 1 |
|
分位数 5 (Quantile 5) |
排名 1 星及以下的股票。这部分股票是我们的机器学习认为表现最差的股票。
分位数 5 =(第五个分位数的几何日收益率)^ (252/1) - 1
|
